(CV-2) Image Enhancement(화질구지 살리기 v1)

어휴... 제목에서 영어만 써서 미안합니다... 저는 한쿡살람임미다! 

이제 화질구지의 이미지를 살리는 방법에 대한 알고리즘을 몇가지 알아보려고 한다. 

 

Concept

개떡같은 화질 혹은 희미한 색을 다른 것들과 분리하거나 경계를 좀 명확하게 해서 구분해보자는 컨셉

MRI나 X-Ray처럼 흑백이 강한 이미지에 쓰면 아주 효율이 좋겠쥬?

Contrast Stretching ==> 명암 대비 ==> Histogram Equlization 이란걸 해볼거다.

Sharpening ==> 테두리 강조 정도로 생각해보자

 

 

Contrast Stretching(명도 대비)

밝은 색은 더 밝게 어두운 색은 더어둡게, 강한 색은 더 강하게 약한색은 더 약하게가 컨셉이다. 

아래 그래프를 보자.

Linear Contrast Stretching/Result

α,β,γ의 기울기를 바꿈으로 색을 어디서 구분할것인지를 선택한다는 컨셉이다. a,b의 위치를 바꿈으로써 직선의 기울기를 바꿀 수 있는데 직선의 기울기가 커지면(α가 커진다고 계산하면) 그만큼 α가 담당하는 영역의 색상이 더 극명하게 구분되는 효과를 낳을 수 있다.

 

Histogram Equlization

 일반적인 컨셉은 아래와 같다. 한부분에 뭉쳐 있는 정보를 평탄하게 펴주는 것인데 이 과정에서 정보의 소실이 일어날 수도 있다. 이 과정은 GrayScale, RGB, HSV,Lab 전부 할 수 있다. 아래는 GrayScale에 대한 평탄화 예시이다.

Histogram Equlization and Result Histogram

HE Procedure/Histogram

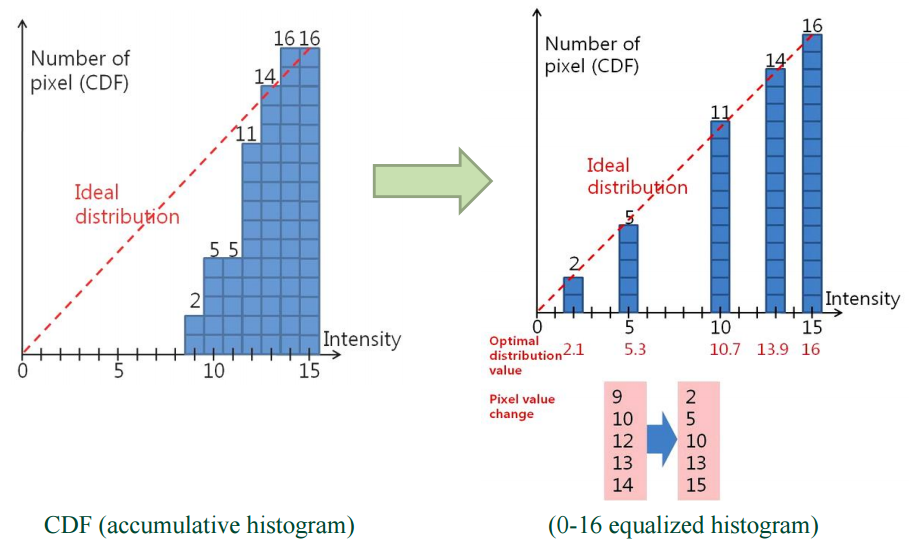
위와 같은 순서로 Equlization을 진행하는데 누적분포를 구하고 그것에 대한 확률함수를 수해서 다시 0~255로 매핑해주는 관점이다. 

근데 이 과정에서 정보 손실이 빈번하게 일어날 수 있다. 500*500이미지에서 0~255 사이의 값중 1이 단 한번만 나온다고 가정하면 1에대한 값은 1/250000이다. HE를 진행하면 1은 그냥 없어지는 값이 된다.

 

두번째 문제는 매핑에서 드러난다. 초기 Histogram이 넓은 분포를 가질 경우(확률분포가 균등분포에 가깝다고 한다면) Equlization해도 의미가 없다... 

 

즉 HE는 히스토그램이 일정 부분에 값이 몰려 있을 경우 효과가 좋다! 라고 생각하면 깔--끔

HSV HE/3 Channel Histogram

HSV색공간에 대한 HE결과는 색깔이 바뀌는 특징을 갖는다. 3채널 히스토그램은 1채널 히스토그램 3개 붙여넣기라고 생각하자. 그게 맘도 편하고 이해하기도 쉽다. 실제로도 각 채널 HE해서 합치는것이다.

 

Adaptive Histogram Equlization(AHE) and Contrast Limited Adaptive Histogram Equlization(CLAHE)

각종 적응형 평탄화 방법이다. 이런거 보면 적응형이 참 신기한것 같기도 하다.

AHE는 패치 크기별로 평탄화를 진행하는 방식/ CLAHE는 최대 한계치를 정해놓고 그걸 넘어서는 수치를 다시 밑바닥에 깔아주는 형식으로 진행된다. 근데 이런 경우 0이 한번도 안나왔는데 CLAHE 진행하면서 없던게 생길수도 있고

적응형이라고 다 좋은것만은 아닌듯 하다.

AHE/CLAHE Histogram

적응형이라고는 하나 딱히 수학적으로 설명할 부분은 크게 없다.

Eqlization은 어차피 각각의 채널에서 따로따로 진행할 것이기 때문이다.

 

 

Sharpening - High Pass filter

이것도 신호처리나 네트워킹에서 들어볼 사람은 들어봤을 용어다. 컨셉도 큰 차이가 없다. 고주파 영역을 더 강조시킨다. 즉 테두리처럼 값이 크게 변하는 영역에 더 큰 값을 주는 방법으로 프로세스가 돌아간다.

수학적 배경/대표적인 High Pass filter

수학적인 배경은 왼쪽과 같다. Δ(x+1)은 1st order과 같다. Δ(t)에서 t=1이므로

f'(x+1) = f(x+1) - f(x)/1

f''(x+1) = f'(x+1) - f'(x)/1 = f(x+1)-f(x) -{f(x) - f(x-1)}/1 = f(x+1)+f(x-1)-2f(x)로 이계도함수의 변화량을 구할 수 있다.

 

우측의 High filter는 2D conv를 생각하면 주변에 비해 높은 값을 갖는 포인트의 값은 커지게 만들어준다는 특성을 갖는 커널을 사용한다고 생각하면 테두리같은 고주파의 경우 더 높은 값을 갖게 될 것이라는 예상을 충분히 할 수 있다.

 

Laplacian 2nd order Derivatives/몇가지 라플라시안 필터

@@라플라시안 필터는 모든 요소값의 합=0 이여야 한다. 

+ Laplacian의 정의는 각각의 이계 편미분계수와 f''에 대한 미분계수가 동일하다는 것을 의미한다.

평범한 공대생들이 배웠을 라플라스 변환과는 차이가 있다.

라플라스 미분방정식이 여기에 맞는 개념일듯

 

Unsharp Mask

High Pass filter/Result

(2)의 두 점에 집중하자 (1)원본 시그널에 Low Pass Filter를 적용하면 (2)그래프가 나온다 (1)-(2) 그래프의 차를 구하면 (3)의 High Pass Filter의 그래프가 나온다. (1)+(3)을 하게 되면 4번의 최종 결과 영상을 얻게 된다.

우측 사진에서 확인할 수 있다.

 

Unsharp Mask Example result/ Original->mask->Original+mask