며칠전에 지인들이랑 관련 대화를 할 일이 있어서 입을 좀 털어봤는데
나름 스스로 개념도 잘 정리되어 있는것 같고 써볼만한 내용이 좀 나올 것 같아서 블로그 내용이 산으로 가기 전에
코드도 보기 전에 얘기좀 해놓고 가려고 한다.
DL에서 여러가지로 해볼 수 있는게 많지만 내가 생각하기에 꽃은 이미지 학습이라고 생각한다.
그리고 그 이미지학습(넘어서는 영상이나 시계열에서도)에서 가장 중요한 개념은 2차원, 3차원 텐서에 대한 합성곱이라서
제발 다들 무턱대고 nn.Conv2D() 쓰기 전에 이 글이 아니더라도 한번쯤 읽어주세요...
이 포스팅에서는 유독 내 손으로 그린 내용이 많을 것같은데 시중에 내가 원하는 스타일에 그림이 없어서 그런거니까
글과 그림이 개떡같아도 양해부탁드린다. 25000원짜리 판 태블릿으로 그리는 중이다ㅎㅎ
Concept
도장찍기!! 합성곱 연산은 도장찍는 것이라고 생각하자.
수학 좋아하는 공돌이인 나도 공학수학에서 라플라스 변환 배울때 했던 합성곱 나오면 라플라스 생각해!!!!!
라고 배웠었는데 수학적으로 틀린말은 아니지만 이게 2D, 3D conv 연산에서는 이렇게 생각하면 와닿지가 않아서
그냥 커널로 도장 찍는 행동이라고 생각하자


Term
Kernel - 찍을 도장이다. CV와 연관지어 얘기한다면 임의의 값을 설정한 여러개의 커널을 학습시켜서 그걸 가지고 이미지의 윤곽선이나 위치 각각의 값을 계산하도록 적응(진화?) 시키는게 결국 딥러닝과 Conv연산의 궁극적 목표라고 할수 있다
Channel - 커널의 종류의 개수, 나는 얘기할때 정보의 페이지 종류의 개수라고 얘기하는데 이것도 뭐 크게 틀린말은 아니지만 어떻게 얘기해도 말로 하는건 직관적이지 않은 것같다.
그래서 몇몇 강사들이 채널을 얘기할때 RGB나 YCMK 또는 GrayScale 얘기를 하면서 각각 3,4,1 채널이다 얘기하는데
난 이거 너무 싫어한다. 그럼 Conv3D에 대한 커널은 어떻게 설명하실건데요?
이렇게 얘기하면 사람들이 아 그럼 색의 기저 종류가 채널 개수 인가봐? 하고 넘어가는데 그건 절대 아니다!!!

위 그림을 보면 채널의 차원을 그려놨는데 1차원은 단순벡터, 2차원은 평면, 3차원은 공간, 4차원은 그럼 시간축까지(근데 이건 못그리는거 다들 알쥬?) 머신러닝에서 벡터의 차원(1,2,3,4~) 이것과는 조금 다르다.
이게 사람눈에는 좀 시각적으로 좋다는 생각이 들고 우리는 앞으로 그냥 저런 데이터에 대해 n차원 텐서라고 통칭 하겠다.
3차원 텐서 보충

만약 위와같은 텐서가 10개 쌓여있는게 하나의 정보인 어떤 3차원 데이터가 있다고 하자
그럼 그 데이터의 차원은 (10,[100,100,100]) 이라고 할 수 있다. 시계열 데이터라서 시간축이 하나 더 있다면
(10,[100,100,100],60) 이라고 할 수 있다.
Convolution 2D
이제 진짜 2차원 합성곱을 해보자. 패딩은 없고 Stride는 1로 생각한다. 이 옵션은 마지막에 Pooling하면서 다루겠다.

이런식으로 모든 칸을 다 채우면 3,3 짜리 결과값이 나온다. (1,5,5) 짜리 데이터가 (1,3,3) 데이터가 되었다. 이게 합성곱의 전부다. 생각보다 거창하게 시작해서 뱀의 머리가 된듯한 기분이네...
Padding and Stride
Padding - 테두리 충전하기
먼저 패딩의 필요성을 알아보자. (5,5)의 데이터가 (3,3)의 데이터로 줄어들었다. 일단 데이터 손실이 발생했다.
더구나 (1,1)은 그 다음 데이터에 단 한번의 기여밖에 하지 못했지만 (3,3)에 '2'는 9번 모두 기여한다. 즉 편향도 발생한다.
이러한 두가지 문제점을 줄이기위해 패딩을 고안했다. 주로 Same Padding을 많이 하는데 위처럼 3X3 커널의 경우
패딩을 상하좌우 1칸씩 채워주면 이후 데이터도 (5,5)로 유지 된다. 이때 전후 데이터의 크기가 동일하여 Same Padding이라고 지칭한다.
Stride - 건너뛰기
위의 예시는 Stride가 1(default)이다. 즉 건너 뛰지 않는다. 만약 stride가 2라면? (2,1)로 시작하는 칸은 도장찍지 않고 넘어간다. 3이면 (2,1),(3,1)을 건너뛰고 (4,1)에서 찍어야하는데 (5,1)이 끝이기 때문에 더이상의 값은 못만들고(1,1)짜리 데이터를 반환한다.
Stride와 Padding의 연산 방법은 다음 Pooling에서 다시 설명하겠다.
Pooling
모델을 만들때 데이터를 압축시키는 방법이다. 주로 MaxPool이나 AvgPool을 많이 한다.
주로 데이터사이즈를 1/2로 줄이는데 쓴다. 채널의 개수는 그대로 유지하면서 행렬 자체를 줄이는데 목표가 있다.
전반적으로 연산은 2차원 합성곱에 기반한다.
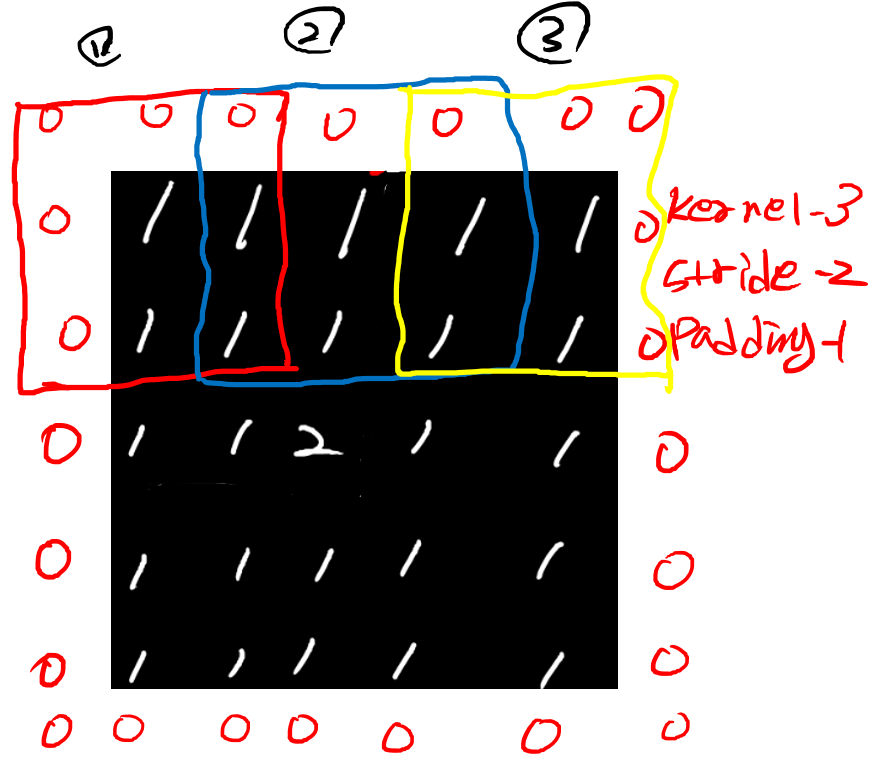
그럼 (1),(2),(3) 세 번 도장이 찍힌다. MaxPooling(4가지 값중에 제일 큰 값을 대표값으로 채택하는 것)
도장이 찍힌 것을 모아 새로운 매트릭스를 만들면 [[1,1,1],[1,2,1]...] 이런 절반으로 줄은 3X3 매트릭스를 반환하게 된다.
Conclusion
결국 Conv 연산은 커널을 학습시키기 위한 일종의 방법이다.
합성곱 연산을 통해 복잡도를 올리기도 하고 풀링을 통해 필요없는 정보를 줄이기도 한다.
이거 말고도 Transport conv도 있다. 이건 나중에 오토 인코더를 다룰일 있으면 그때 해야징 ㅎㅎ
'Python and Data' 카테고리의 다른 글
| (CV-5)image transform and DCT-DiscreteCosineTransform-1 (0) | 2023.08.21 |
|---|---|
| (CV-4)Edge Detection and Canny Edge Detector(화질구지 살리기 v3) (0) | 2023.08.16 |
| (CV-3)Noise Reduction 각종 필터(화질구지 살리기 v2) (0) | 2023.08.15 |
| (CV-2) Image Enhancement(화질구지 살리기 v1) (0) | 2023.08.14 |
| (CV-1)CV 밑바닥(진짜밑바닥은아님)부터 시작하기(색공간과 유사도) (2) | 2023.08.14 |



