이제 화질구지를 탈출했다.
근데 며칠전에 친구들이랑 얘기를 해보니까 화질구지를 모르는 사람이 많더라 그래서 짤하나 방출
간단한 상황설명은 2G 피처폰 시절(롤리팝폰도 나오기 전) 카메라 화질이 몹시 안좋았는데 첫 답변자가 화질이 구리다는 말을 띄어 쓰기 안하고 써서 그 뒷사람들이 아는척 하려고 하다가 나온 짤이다...(나만 웃겨요..?)
Concept
지금까지 사용했던 이미지의 각 픽셀의 색을 다른 신호로 바꾸는 것을 의미한다.
주파수로 바꿔서 송수신을 할 수도 있고 또다른 행렬로 바꿀 수도 있다.
데이터의 양을 줄이고 패턴을 분석하는데 그 의의가 있다.
DCT를 통한 JPEG압축, Harr Transform, Gabor Transform등이 있다.
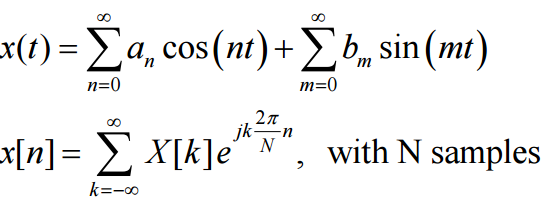
각각의 Transform algorithm을 배우기 전에 수학적인 바탕을 보고 가자.
푸리에 변환에 대해 안다면 아래로 쭉 내려가면 된다.
푸리에 변환은 신호시스템의 관점과 수학적 관점 두가지로 접근할 수 있다.
신호시스템적 관점에서는 어떤 특정 파동개형을 갖는 신호를 여러 다른 종류의 주파수를 갖는 개형의 파동(일반적으로는 sin, cos개형에 주기와 진폭만 변조한 개형들)의 합으로 나타내는 것을 의미한다.
수학적인 관점에서는 푸리에 급수로 거슬러 올라간다. 어떤 하나의 함수가 있다고 상정했을 때 cos,sin함수의 값으로 원함수에 근사하도록 그래프 개형을 만드는 것을 의미한다.
이 두가지 모두 컨셉은 유사하다. 어떤 함수 또는 파동(즉 데이터)에서 우리가 잘 알고 있거나 다루기 편한 다른 여러 함수의 합으로 원 데이터를 "분리"해 내겠다는 것이다.
그래서 위 함수의 cos과 sin함수는 변환의 기저(basis, 좌표계의 기준)이 된다. 이때 각 기저인 cos(nx), sin(mx)는 n,m이 모두 정수라고 가정하면 dot(cos(nx),sin(mx)) = 0 이므로 Orthogonal 하다.
결론은 하나의 원본 데이터를 Cos함수의 n주기를 갖는 여러 함수의 그래프+Sin함수의 m주기를 갖는 여러 함수의 그래프로 분리하겠다는 것이 목적이다.
DCT(Discrete Cosine Transform)
이산 코사인 변환이다. 목표는 특정 파형을 코사인 함수로 분해한다는 점에서 지금까지 얘기한 컨셉과 동하다.
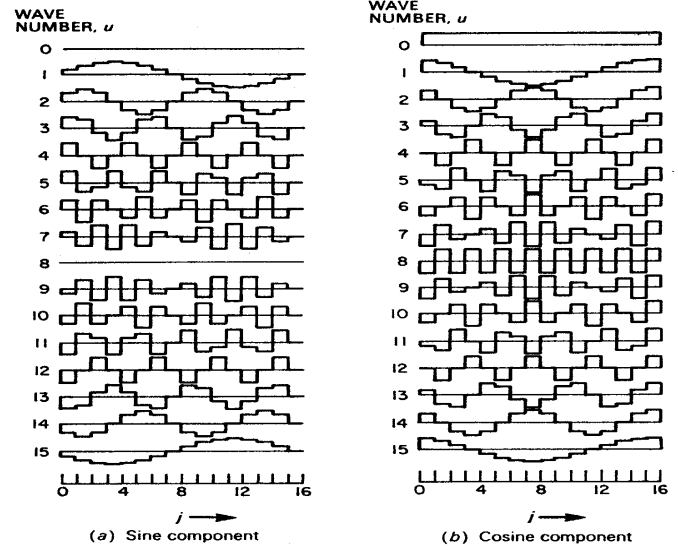
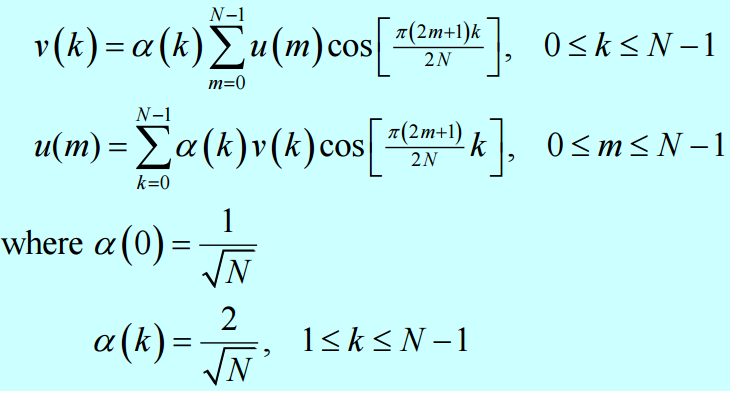
위 가장 왼쪽 그래프는 각각 sin, cos분해를 의미하며 중간의 수식은 1차원 DCT 변환의 DCT 계수를미한다.
이때 u(m) = Pixel Intensity, v(k) = cos DCT의 계수 n을 의미하며 변환시 파형 자체를 저장하는 것이 아니라 v(k)를 저장,
송신하고 이를 수신, 다시 복조하여 동일한 데이터를 재생산할 수 있다.
2차원 DCT
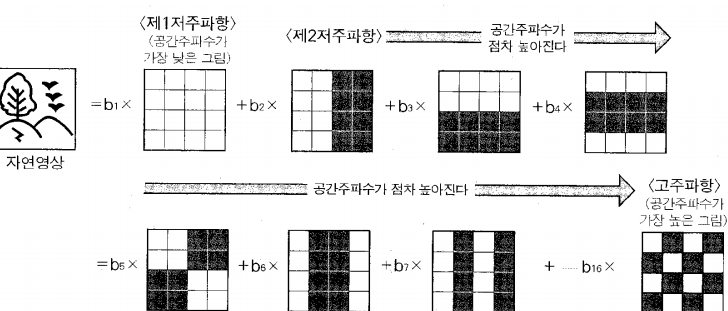
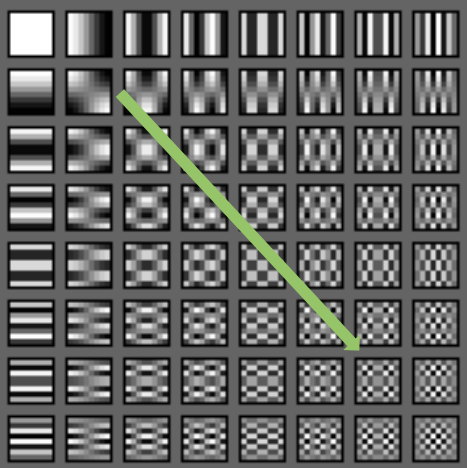
2차원 데이터(이미지)에 관한 DCT 필터를 통한 데이터 압축은 다음과 같다. 가로로 흐르는 파동 하나를 넣은 패턴, 세로로 흐르는 파동 하나를 넣은 패턴... 이런 꼴로 점차 패턴 자체의 복잡도와 주파수를 높이는 방식으로(결국 변화도 Δx가 높은 값들이 우측 아래 화살표 방향에 포함된다.) 패턴을 디자인 한다.
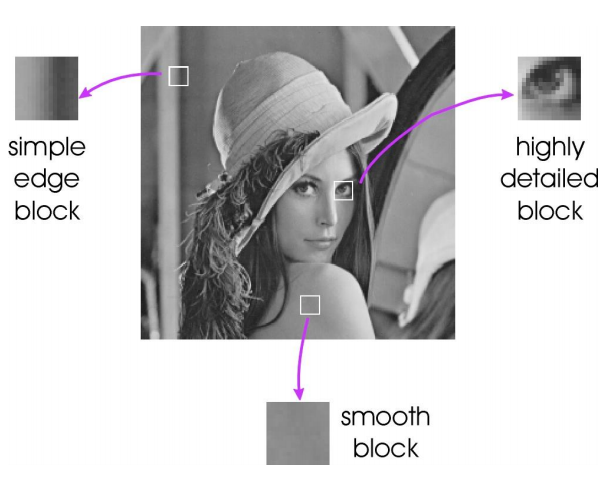

예시를 보면 다음과 같다. 세가지 포인트는 누가봐도 주파수가 크게 다르다.(인정?) 우측 자료를 보면 주파수가 낮은
포인트는 적은 DCT 필터중 몇 부분 활성화 되지 않았다. 하지만 고주파 영역의 포인트로 갈 수록 많은 수의 DCT 필터(특히 고주파 영역에도 포함되는) 것들이 활성화되는 모습을 확인할 수 있다.


coef에 log에 1을 더해주는 이유는 log 0 = -inf 이기 때문에 0이 만들어지는 상황을 피하기 위함이다.

특정 임계값을 넘긴 값들에 대한 양자화를 진행한 결과는 다음과 같이 정보가 압축된다. 음수 혹은 작은 값을 가진 데이터는 coef공식에 따라 0~1 사이로 수렴하고 지나치게 큰 값을 가진 값은 스케일링 된다. 다음 과정을 통해 데이터의 손실이 일어날 수 있으며 JPEG2000 또한 이 방법을 채택하고 있다.
Quantization(양자화)에 대한 부분은 다음 포스팅에서...
'Python and Data' 카테고리의 다른 글
| (Python-Django)Django 빠른 습득기-0 (1) | 2023.10.14 |
|---|---|
| (CV-6)image transform and DCT-2 and Harr, Gabor Transform (0) | 2023.08.22 |
| (CV-4)Edge Detection and Canny Edge Detector(화질구지 살리기 v3) (0) | 2023.08.16 |
| (ML/DL-3)2차원 합성곱과 기본 연산(Conv2d and Pooling) (0) | 2023.08.15 |
| (CV-3)Noise Reduction 각종 필터(화질구지 살리기 v2) (0) | 2023.08.15 |


