(CV-6)image transform and DCT-2 and Harr, Gabor Transform

Concept

 

이걸 왜하는지에 대한 목적을 한번 살펴보자. 아래의 과정을 거쳐 데이터를 압축했다가.

잘 전달해서 가능한한 손실없이 풀어보는데 그 의의가 있다. 우리는 그 과정중에 있으며 이제 DCT하나 했다.

이제 데이터의 양을 알고리즘에 대입해 줄이는 방법에 대해 생각해본다.

JPEG Encoding Structure

Quantization

DCT 이후 양자화 방법에 대해 생각해보자. 목적은 데이터의 종류를 획기적으로 줄이는데 있다.

 

Zigzag Scan

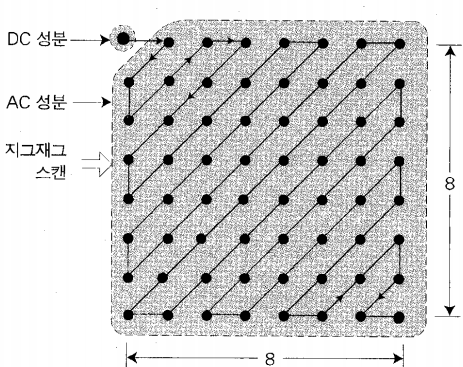
내가 전부터 쓰긴 했지만 언급하지 않았던 내용이 있었다.  DC는 저주파 성분, AC는 고주파 성분이다. 

Zigzag Scan은 DC성분과 AC성분으로 이미지를 분리하고 RLE(Run length Encoding)을 통해 각각의 성분을 따라가며  데이터의 양을 줄일 수 있다. 다음의 자료를 보자.

지그재그 스캔 예시

 

Entropy coding(Huffman Algorithm)

 

Huffman coding의 컨셉은 동명의 알고리즘과 똑같다. 나오는 빈도가 잦은 데이터는 적은 양의 비트에, 잘 나오지 않는 데이터는 큰 비트에 할당함으로써 총 데이터의 양을 줄이는 것을 말한다. 즉 발생 확률과 각 데이터의 비트수를 반비례 관계에 두고 대치 시키는 것을 의미한다. 아래 자료를 보자.

일반적 인코딩/허프만 코딩

위와 같은 방식으로 비트를 할당하는 알고리즘을 사용하면 확률이 한쪽으로 치우쳐져 있을때 극한의 정보 이득을 볼 수 있다. 하지만 모든 데이터가 균등 분포에 가까운 확률 분포를 보인다면 허프만 알고리즘은 전혀 도움이 되지 않는다는 한계가 있다.

 

 

Harr Transform

 

Harr Transform의 공식은 다음과 같다. 공식에 따라 변환 행렬을 정립할 수 있지만 계산을 하나하나 하긴 귀찮으니

구글링과 공식의 암기를 적절히 병행하도록 하자.

harr transform의 공식/공식으로 유도된 변환계수 행렬

Harr Transform의 컨셉은 패턴인식과 같은 특정 지역의 처리에 특화되어있다는 장점이 있다. 

기저로는 DCT의 8X8 패치를 사용하더라도 특정위치의 인식에는 Harr Transform이 효과적이다.

아래 자료는 Harr Transform의 그래프에 비트 표현을 추가한 것이다.

비트 표현을 추가한 그래프/주로 사용하는 Harr filter 

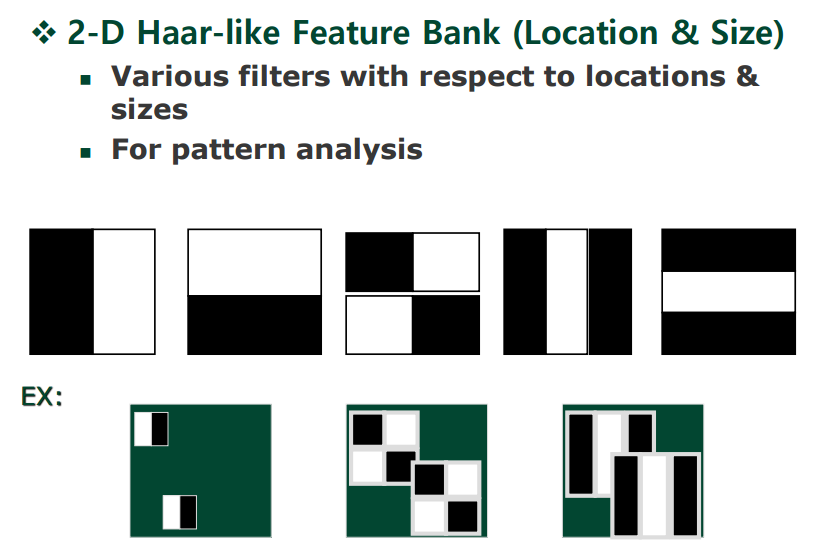
우측의 Harr filter을 사용하여 아래의 예시처럼 크기에 맞게 다양한 Harr filter를 적용하여 값을 구할 수 있다.

 

Gabor Transform

 

Gabor Transfrom의 수학적 기반은 다음과 같다. (지금 나도 잘 모르겠는데 모종의 이유로 CV관련 포스팅을 한번에 많이 해야해서 막 쓰는데 나중에 다 지우고 다시 쓸거다.)

 

전반적인 컨셉은 Harr 처럼 부분적인 패턴을 인식하겠다는 것에 큰 차이가 없지만 패턴의 회전또한 인식하겠다는 점에서 장점을 갖는다.

 

1차원/2차원 Garbor filter의 수식

 

가우시안 필터와의 차이는 다음과 같다. 특히 우측의 Garbor fitler를 모아놓은 자료를 보면 회전하고 있다는 느낌을 확실하게 받을 수 있다.

일반적인 Gaussian filter와 Gabor filter의 차이/Garbor filter 모음집